前缀和、哈希表

题目

给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

示例 1 :

输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :

数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ，且整数 k 的范围是 [-1e7, 1e7]。

题解

分析

题目要求为求出连续的子数组的和等于k，那么问题即为求nums[i:j]元素和使其等于k

如果重复计算nums[i:j]，暴力的话可以重复遍历该数组，试想若能在O(1)时间内快速得出nums[i:j]元素之和？

思路：

前缀和的思路是这样的，对于一个给定的数组 nums，我们额外开辟一个前缀和数组进行预处理：

1
2
3
4
5
6
nums=[3,5,2,-2,4,1]
n = len(nums)
preSum=[0]*(n+1) # 前缀和数组
for i in range(n):
    preSum[i+1]=preSum[i]+nums[i]
preSum
[0, 3, 8, 10, 8, 12, 13]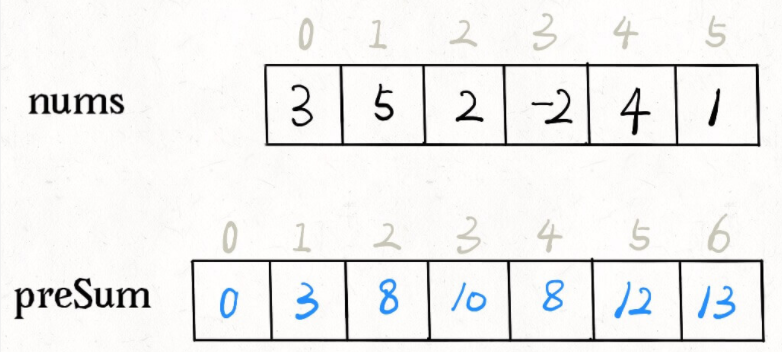

这个前缀和数组 preSum 的含义也很好理解，preSum[i] 就是 nums[0:i-1]的和。那么如果我们想求 nums[i:j] 的和，只需要一步操作 preSum[j+1]-preSum[i] 即可，而不需要重新去遍历数组了。

回到这个子数组问题，我们想求有多少个子数组的和为 k，借助前缀和技巧很容易写出一个解法：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def subarraySum(self, nums, k) -> int:# nums: List[int], k: int
        n = len(nums)
        # 创建前缀和数组
        preSum=[0]*(n+1)
        for i in range(n):
            preSum[i+1]=preSum[i]+nums[i]
        
        ans = 0  # 返回值等于k的个数
        for i in range(1,n+1):
            for j in range(i):   
                if preSum[i]-preSum[j]==k:
                    ans +=1
        return ans
1
2
3
4
5
nums=[1,1,1]
k=2
a = Solution()
answer =a.subarraySum(nums,k)
print(answer)
2

时间复杂度为$O(n^2)$，空间复杂度$O(n)$

提交leetcode超出时间限制

优化

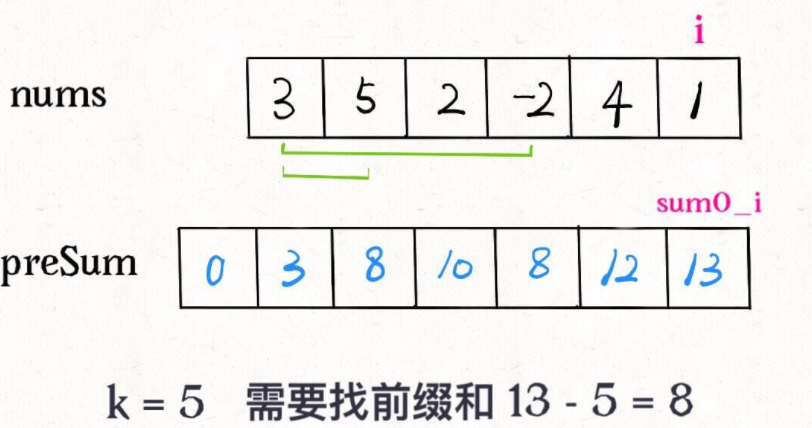
分析满足条件preSum[i]-preSum[j]=k，其实也即满足条件preSum[j]=preSum[i]-k

优化思路：我直接记录下有几个 preSum[j] 和 preSum[i] - k 相等，直接更新结果，就避免了内层的 for 循环。我们可以用哈希表，在记录前缀和的同时记录该前缀和出现的次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def subarraySum(self, nums, k) -> int:# nums: List[int], k: int
        n = len(nums)
        # 以字典方式构造前缀和数组
        preSumdict={0:1}
        ans=0 # 返回与k相等的子数组和个数
        sum0_i=0
        for i in range(n):
            sum0_i +=nums[i]
            # 我们要寻找的前缀和nums[0:j]
            sum0_j=sum0_i-k
            # 如果前面有这个前缀和，则直接更新答案
            if sum0_j in preSumdict.keys():
                ans += preSumdict[sum0_j]
            # 把前缀和nums[0:i]添加至前缀和字典中
            if sum0_i in preSumdict.keys():
                preSumdict[sum0_i]+=1
            else:
                preSumdict[sum0_i]=1
        return ans
1
2
3
4
5
nums=[1,1,1]
k=2
a = Solution()
answer =a.subarraySum(nums,k)
print(answer)
2

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://fishni.github.io/2021/05/11/LeetCode-I-%E5%85%B6%E4%BB%96%E7%AE%97%E6%B3%95-%E5%89%8D%E7%BC%80%E5%92%8C%E6%8A%80%E5%B7%A7-560.%20%E5%92%8C%E4%B8%BAK%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84/