之前做LineCTF2021-babycrypto3题时,知道明显是RSA的大整数分解,使用了各种方式,未果,事后了解到GGNFS和MSIEVE分解因数
本文就各种可能状况的分解进行简单介绍,并详细介绍一些工具的安装使用,以及针对带有pub.pem的公钥文件的RSA题进行简单总结
Table of Contents
知道RSA算法的应该都知道公钥(n,e),如果能有效分解模数n,那么其私钥(d,p,q)我们就能获得,所以这时其就不具备安全性。但是当n为较大整数时,基于大整数分解困难,又能保证RSA是安全的。但是对大整数的分解一直被研究,相关算法有Pollard Rho算法、连分数算法(Continued fracion,CFRAC)、二次筛法(Quadratic Sieve,QS)、平方型分解法(SQUFOF)、椭圆曲线(ECM)和数域筛法(Number Field Sieve,NFS)等,有感兴趣的可以了解相关算法。根据参考文献【1】,目前有700多位(二进制)被分解,但耗时也是非常非常长的。之前做LineCTF2021-babycrypto3题时,知道明显是RSA的大整数分解,使用了各种方式,未果,事后了解到GGNFS和MSIEVE分解因数
本文就各种可能状况的分解进行简单介绍,并详细介绍一些工具的安装使用,以及针对带有pub.pem的公钥文件的RSA题进行简单总结
RSA整数分解场景
假设我们从题目获得了公钥(N,e)和待解密的密文c,由RSA的加解密过程,我们知道,如果要解密密文,我们要得到e的逆元d,而d是要我们去求解的。
若n较小,直接分解
若n较大,在线分解:http://factordb.com
yafu工具分解
适用情况:p和q相差较大或相差较小时,可快速分解GGNFS和MSIEVE分解
可使用RsaCtfTool
一般题目中,若是可分解,使用yafu或者msieve即可分解。若是有迹可寻,也即特殊情况下,可使用相关脚本解
n较小,直接分解几种算法
短除法
- 短除法1
1 | # -*- coding: utf-8 -*- |
24
[2, 2, 2, 3]- 短除法2
1 | # -*- coding: utf-8 -*- |
21
[3, 7]Miller-Rabin素性测试和离散对数Pollard_rho分解
1 | # -*- coding: utf-8 -*- |
33
len: 2
Counter({3: 1, 11: 1})n较大,在线查找
当n较大时,若用常用的工具无法分解,可利用在线网站:http://factordb.com
Wiener’s attack
适用情况
适用情况:e过大或过小。
在e过大或过小的情况下,可使用算法从e中快速推断出d的值。详细的算法原理可以阅读:低解密指数攻击
https://www.tr0y.wang/2017/11/06/CTFRSA/index.html#%E4%BD%8E%E8%A7%A3%E5%AF%86%E6%8C%87%E6%95%B0%E6%94%BB%E5%87%BB
wiener’s attack代码参考:https://github.com/pablocelayes/rsa-wiener-attack
下面内容摘自上面参考博客
简单介绍


代码
- python2代码
1 | # -*- coding: utf-8 -*- |
('e', 14065324093316017945695720258347429532521523200228598193322667338820770590989154977786981894794588594064536009186732255775035804405327706425255296803855527639374329558376563095664859692148197185703687276097309462020144376262777557533944519562049109221719648126706993033163993490190085491702629251352329396471456129542825658446009162968346786594848548139595669836329358788165100849817671092568134531593182392252696719165573226130084180843486935720502707239300540428534291779101061922644007823991998086019198292035392258539304441052201138357754863223836486846439513422901513872417295274198920142360883876210212927825007L, 'n', 18462906143035540993814517057095163128283817787230664517838986634801013392767711846485937113330072380038567780269061919808605648774959966319179757205173372523095161810322702620470126948608656351385935375720727519176775110406692586449768317335765421930399299578230419560189633716571287406027463911286833332787737419540756653612611709926058384814812935770145166745335145087323852211057246522872067333040272572190577262813212787729743380140592301701193918348912668992966189995193003441075512789075254845693251194059243188025613215624222354768281910170062917473229700929505219308776883069798326608764552258161920559190481L)
[+]Found!
[-]p = 104235442847969552884769987994197297422543352176802940317177677000499807722195632069286150361214879780730339973882703487096199834739930880687593938040395436586345480730212942206420793142692112306639438014319225266407401819137390988067078857106773391577174349673013152862143650835518682246788303050611999452911
[-]q = 177126950666523578738984064380839651168608739644946060823792396091708111322051866642111785827074573440159197219479475538437582278979185941268904558179007415168216637577906599474105547898107223364283435084419522228187779674837611069387527478313869377950991632158274789401880909076604812300066218450595389655871
[-]n = 18462906143035540993814517057095163128283817787230664517838986634801013392767711846485937113330072380038567780269061919808605648774959966319179757205173372523095161810322702620470126948608656351385935375720727519176775110406692586449768317335765421930399299578230419560189633716571287406027463911286833332787737419540756653612611709926058384814812935770145166745335145087323852211057246522872067333040272572190577262813212787729743380140592301701193918348912668992966189995193003441075512789075254845693251194059243188025613215624222354768281910170062917473229700929505219308776883069798326608764552258161920559190481
[-]d = 42043
[-]m is:flag{w13n3r_4tt4ck_d_1s_10w}
[!]Timer: 40.97 s
[!]All Done!费马分解
适用情况
当大整数N的两个因子p和q相近时,我们可以通过费马分解的办法很快分解大整数
代码示例
1 | from isqrt import isqrt |
p: 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928997877221
q: 31093551302922880999883020803665536616272147022877428745314830867519351013248914244880101094365815998050115415308439610066700139164376274980650005150267949853671653233491784289493988946869396093730966325659249796545878080119206283512342980854475734097108975670778836003822789405498941374798016753689377992355122774401780930185598458240894362246194248623911382284169677595864501475308194644140602272961699230282993020507668939980205079239221924230430230318076991507619960330144745307022538024878444458717587446601559546292026245318907293584609320115374632235270795633933755350928537598242214216674496409625928797450473
flag{d1fference_between_p_And_q_1s_t00_5mall}GGNFS和MSIEVE分解
windows下安装
官网:http://gilchrist.ca/jeff/factoring/nfs_beginners_guide_perl.html
以及翻译:https://bbs.pediy.com/thread-156206.htm
- 使用Number Field Sieve(NFS)算法分解大于90位的数字,我们可使用GGNFS和MSIEVE软件工具来完成此任务。
- 对于小于90位的数字,应将二次筛(QS)与MSIEVE或YAFU之类的程序一起使用。
- 为要分解的数字大小选择一个合理的分解算法很重要。例如,下面的100位整数使用ECM算法花费了将近80天的时间,而GNFS仅需几个小时。同样,少数数据应使用除GNFS之外的其他因素(例如ECM或QS)进行分解。
下面示例:如何使用通用数字字段筛(GNFS)和Brian Gladman的factmsieve.py python脚本同时使用ggnfs和msieve工具对以下100位整数进行因子分解:2881039827457895971881627053137530734638790825166127496066674320241571446494762386620429538
ECM在线和windows下yafu分解测试
- ECM在线分解大整数:https://www.alpertron.com.ar/ECM.HTM
ECM和SIQS(二次筛法)结合
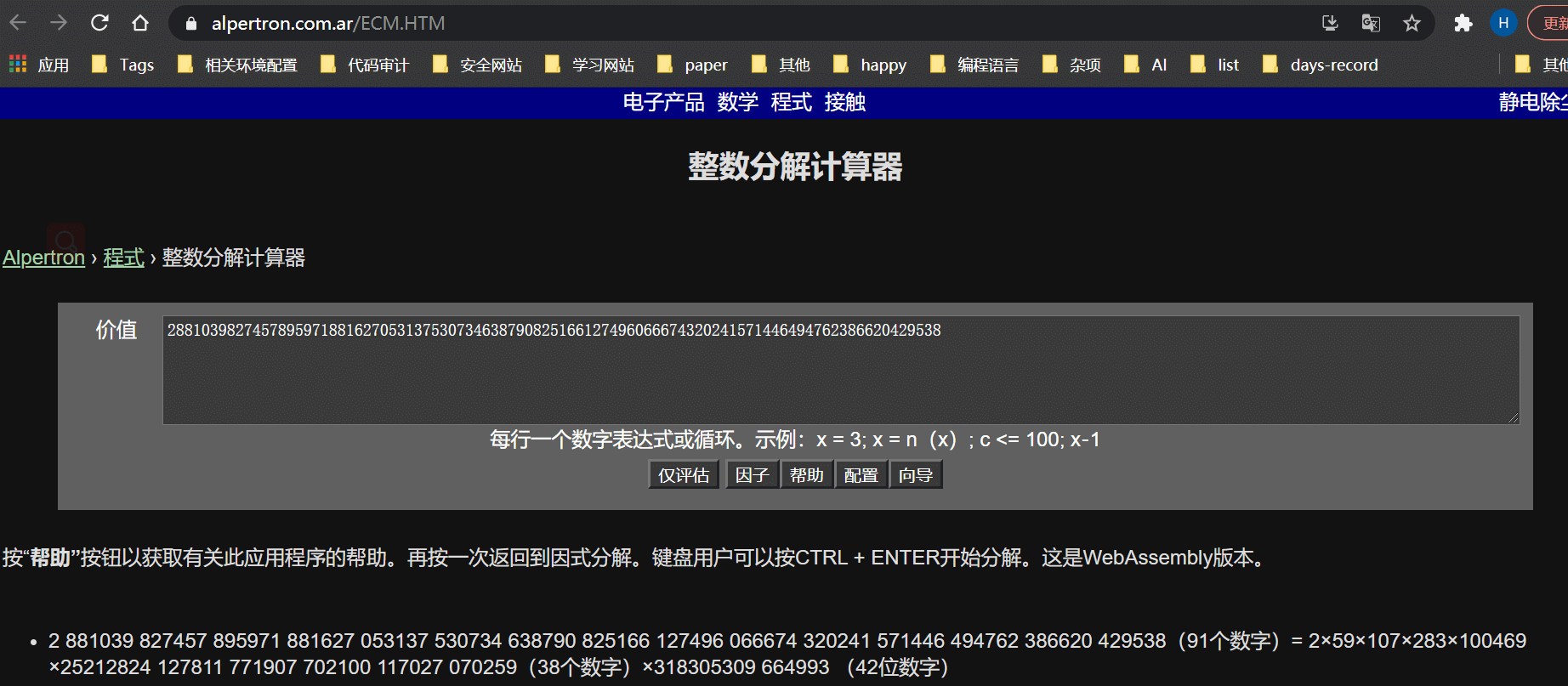
在线ECM测试结果:2 881039 827457 895971 881627 053137 530734 638790 825166 127496 066674 320241 571446 494762 386620 429538(91个数字)= 2×59×107×283×100469 ×25212824 127811 771907 702100 117027 070259(38个数字)×318305309 664993 (42位数字)
用时:12m 21.4s
- yafu分解测试
输入.yafu-x64.exe后回车再输入factor(number)
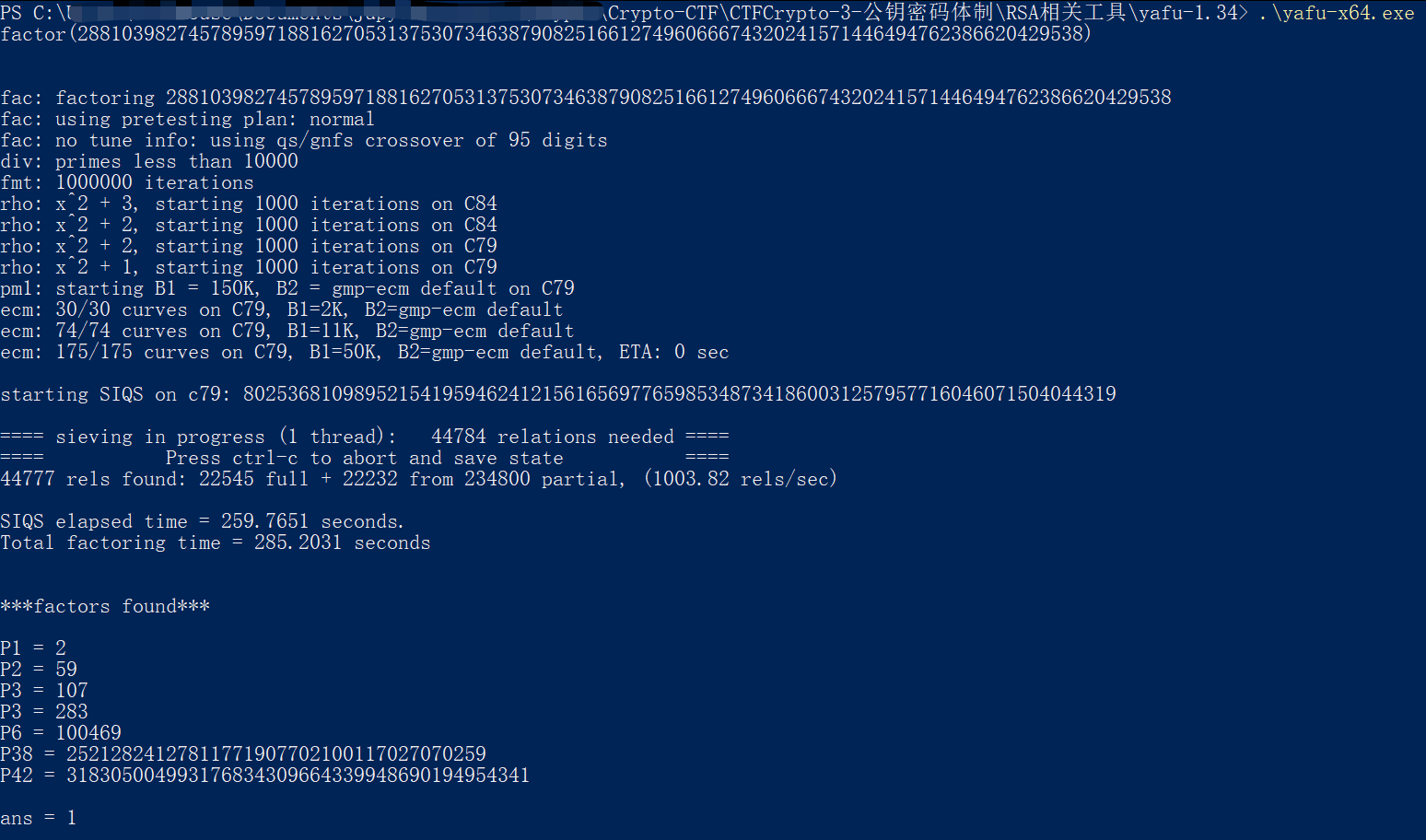
用时285.2031秒
下载msieve
下载地址:https://sourceforge.net/projects/msieve/
下载完后将其内容复制添加至ggnfs文件夹中
下载ggnfs
- 先下载:factmsieve.py
参考链接:http://brg.a2hosted.com/oldsite/computing/factmsieve.py
- 再下载ggnfs
下载地址:https://sourceforge.net/projects/ggnfs/
因为我的电脑是windows自动检测下载的exe文件,然后下载即可
下载完成ggnfs文件夹内容如下图:下载后并没有def-nm-params.txt和def-par.txt这两个文件
可从网站:https://github.com/MersenneForum/ggnfs/tree/master/bin 中下载这两个文件
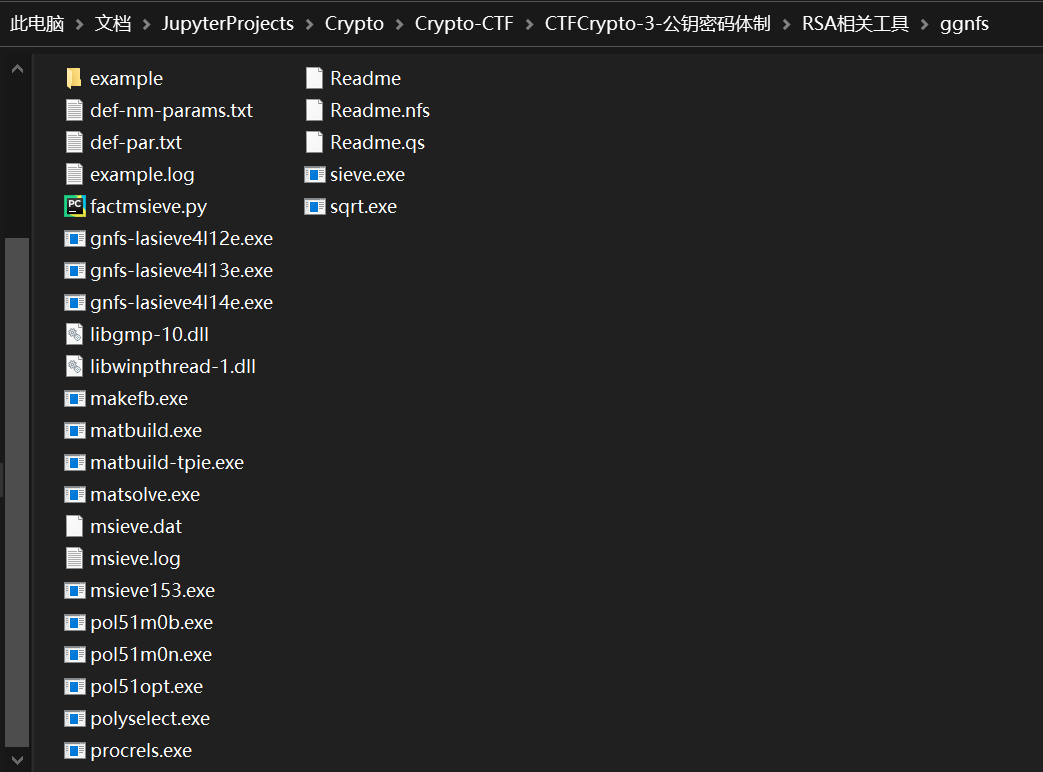
- 创建一个工作目录C:xxxxxx\ggnfs\example
修改factmsieve.py文件
使用notepad++修改factmsieve.py文件
Change lines 63-64 from:
Set binary directory paths
GGNFS_PATH = ‘C:/Users/brg\Documents/Visual Studio 2015/Projects/ggnfs/bin/x64/Release’
MSIEVE_PATH = ‘C:/Users/brg/Documents/Visual Studio 2015/Projects/msieve/bin/x64/Release’to:
Set binary directory paths
GGNFS_PATH = ‘../‘
MSIEVE_PATH = ‘../‘
- 查看自己电脑的CPU核数,命令行输入 wmic ,再输入cpu get
C:\Users\xxx>wmic
wmic:root\cli>cpu get滑动底部得到,如图所示:
修改67 from:
NUM_CPUS = 4
to 若你的CPU为双核,可选1或2;若为四核,则可选1,2,3,4
NUM_CPUS = 4默认情况下,factmsieve.py将使用msieve进行多项式选择。普通用户应该保留这个设置。如果出于某些原因,你想使用pol51多项式选择工具更做下面更改
change lines 89-90 from:
USE_KLEINJUNG_FRANKE_PS = False
USE_MSIEVE_POLY = True
to:
USE_KLEINJUNG_FRANKE_PS = True
USE_MSIEVE_POLY = FalseGPU
如果您使用的是启用了 GPU 的 msieve 版本,并且希望使用 GPU 启用多项式选择,请修改第 70 行,确保它写着。
USE_CUDA = True
如果您没有使用GPU,请确保它写着:
USE_CUDA = False在第104行,如果你使用的不是’msieve’,请确保你的msieve可执行文件被正确命名。我的是msieve153故这里改为msieve153
MSIEVE = ‘msieve153’
由于我的本机运行出错,故将CUDA设置False
进入下一步
多项式选择
NFS算法采用了3个阶段的方法,首先是多项式选择,然后是筛分,最后是线性代数。 在分解开始之前,必须先选择一个多项式。
factmsieve.py脚本将运行适当的工具为你选择一个。
windows下在上面创建的example文件夹中,创建example.n文件,该文件内容为:
n:2881039827457895971881627053137530734638790825166127496066674320241571446494762386620442953820735453
windows在example工作目录运行:
C:xxxx\ggnfs\example> python ..\factmsieve.py example如下图: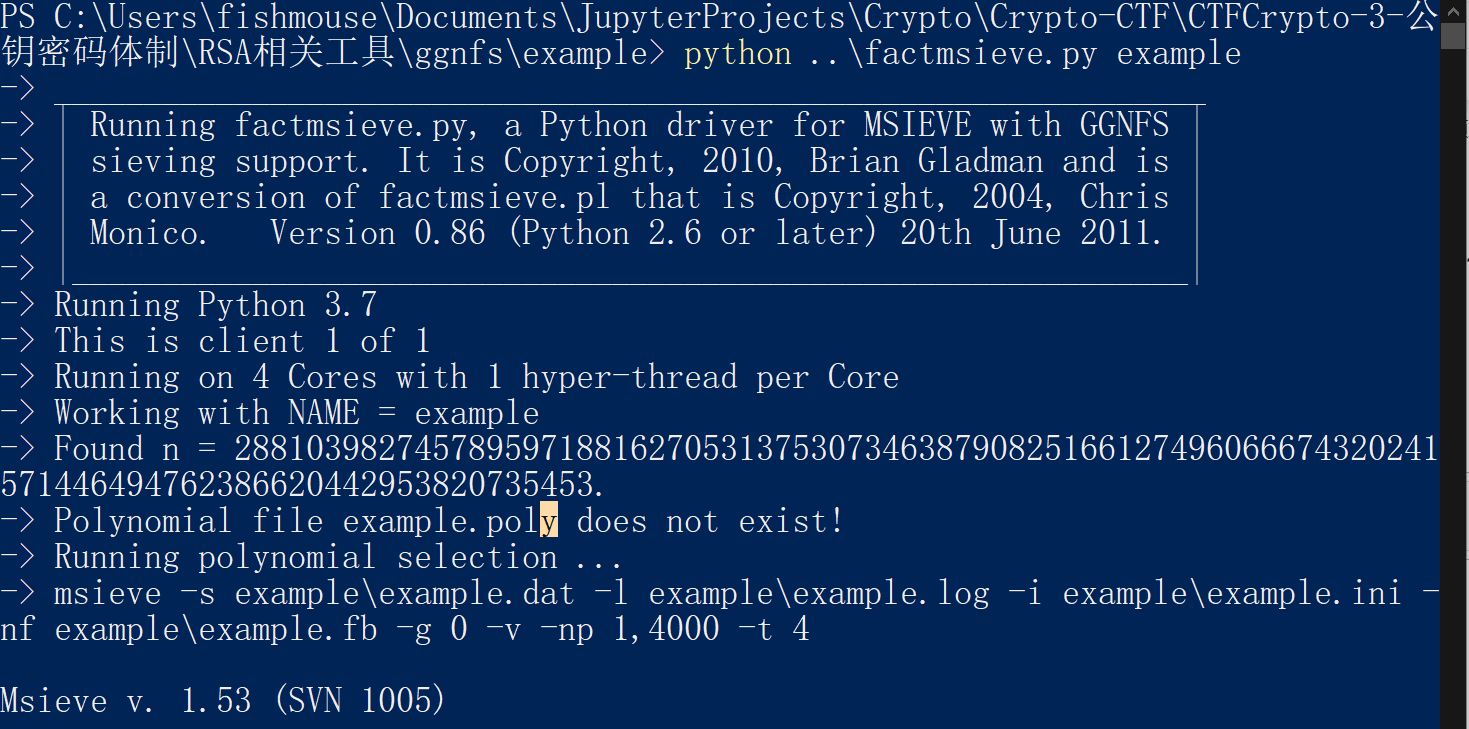
至此windows下已安装完成
Linux下安装
下载msieve:https://github.com/MersenneForum/msieve
其中包含了gnfs我们就直接在该文件夹下,终端输入make all即可
我使用的是kail所以命令如下:
root@kali:~/myctf/msieve# make allCADO-NFS安装
CADO-NFS是C / C ++中数字字段筛选(NFS)算法的完整实现,用于分解整数并计算有限字段中的离散对数。它包含与算法所有阶段相对应的各种程序,以及可能在计算机网络上并行运行它们的通用脚本
下载镜像
下载mitchelldehaven/cado-nfs镜像,大约1个G
docker pull mitchelldehaven/cado-nfs运行容器,打开交互界面,进入/bin/bash目录,然后再进入/cado-nfs-2.3.0目录
docker run -it mitchelldehaven/cado-nfs /bin/bash
这个镜像预先是没有make的,所以需要make,等一会即可
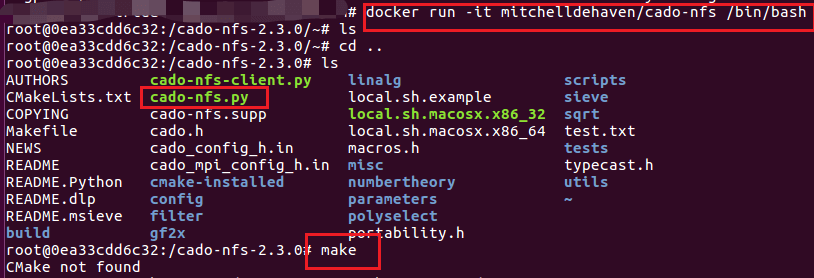
简单测试:分解
90377629292003121684002147101760858109247336549001090677693
1 | ./cado-nfs.py 90377629292003121684002147101760858109247336549001090677693 |
260938498861057 588120598053661 760926063870977 773951836515617
题目-LineCTF2021-babycrypto3
Plesase decrypt and get flag.
Flag is LINECTF{
decrypted text is human-readable text.
- 附件:ciphertext.txt和pub.pem
题解
分析密文
- ciphertext.txt文件内容
1 | with open('ciphertext.txt','rb') as f: |
b'\x01\x14\x1fUxa\xaa\xb3C\x9b\xe1\xeb\x87\xa0\x12`\x156e\x8a\x05\xf4\xf3x\xf7\xb9\xda\xe5J\x08Cn\\C]V\xdd\x1bH\x96\xb74\xae\xcd\x83\x88A\xd5\x92&'- 将字节转换为整数
1 | from Crypto.Util.number import long_to_bytes, bytes_to_long |
10879776433900426660843740332190892429769159527203392037251077478777616065501519198653853699716123394455804888854401574解析公钥文件
方式1:OpenSSL软件
命令:rsa -pubin -in pub.pem -text -modulus如图
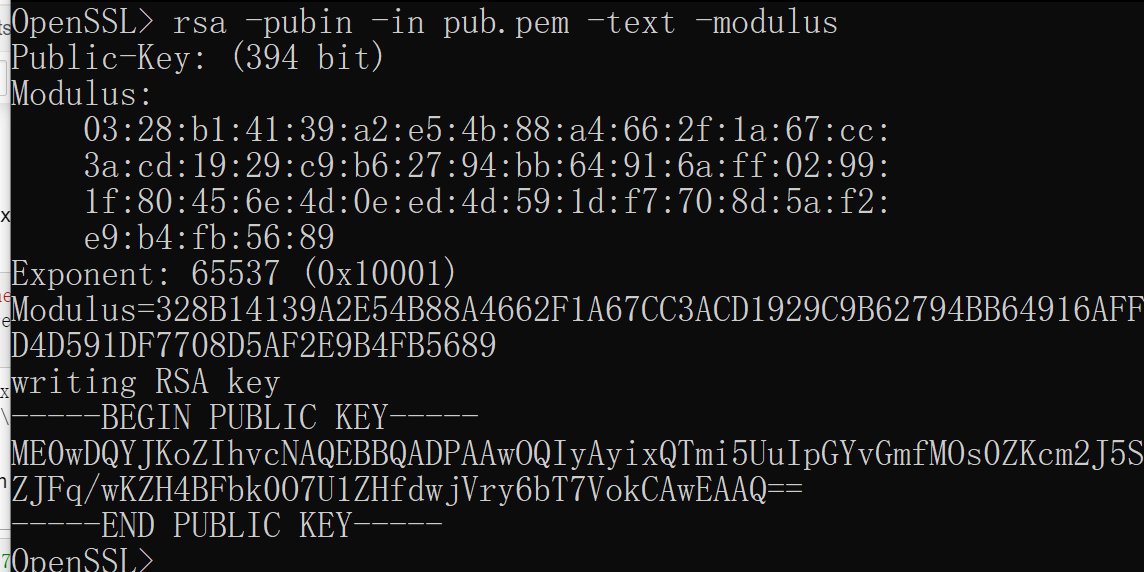
方式2:Python库RSA
- 获取公钥(e,n)
1 | from Crypto.PublicKey import RSA |
(65537,
31864103015143373750025799158312253992115354944560440908105912458749205531455987590931871433911971516176954193675507337)分解n
查看n的位数
1 | len(bin(n))-2# bit |
394说明可分,首先在http://factordb.com 查找,比赛时是查不出来的,目前已经有提交给这个网站,故现在是可查的
由于本机线程过小,跑的时间过长就直接粘贴网址查询的p和q
1 | p = 291664785919250248097148750343149685985101 |
解密
- 由上文已知,n,e,p,q
直接利用RSA加解密原理
1 | import libnum |
b'\x02`g\xff\x85\x1e\xcd\xcba\xe5\x0b\x83\xa5\x15\xe3\x00Q0xPU0lORyBUSEUgRElTVEFOQ0UuCg==\n'- 观察到有base64编码
1 | import base64 |
b'CLOSING THE DISTANCE.\n'可知flag为:LINECTF{CLOSING THE DISTANCE.}
- 完整代码
1 | from Crypto.PublicKey import RSA |
31864103015143373750025799158312253992115354944560440908105912458749205531455987590931871433911971516176954193675507337 65537
b'\x02`g\xff\x85\x1e\xcd\xcba\xe5\x0b\x83\xa5\x15\xe3\x00Q0xPU0lORyBUSEUgRElTVEFOQ0UuCg==\n'参考文献
[1]王兴波,唐春明,李建辉.公钥密码体制中大整数分解算法研究[J].现代信息科技,2020,4(16):125-133.
https://github.com/x-vespiary/writeup/blob/master/2021/03-line/crypto-babycrypto3.md





