深度优先搜索、回溯思想
题目
n皇后问题研究的是如何将n个皇后放置在$n\times n$的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数n,返回所有不同的n皇后问题的解决方案。
每一种解法包含一个不同的n皇后问题的棋子放置方案,该方案中‘Q’和‘.’分别代表了皇后和空位
示例 1:
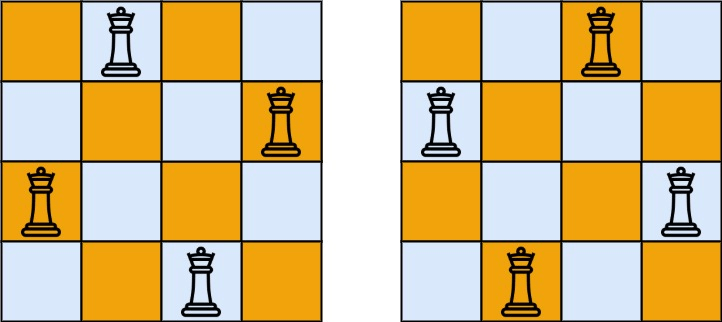
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。示例2:
输入:n = 1
输出:[["Q"]]题解
简要分析:我们首先可以知道不能相互攻击也即
- 同一行,同一列只能有一个皇后
- 且任何两个皇后都不能在同一条斜线上
我们可以使用回溯法求解
第一个皇后有N个选择,第二个则有N-1个选择,依次推得所有可能的情况不会超过 N! 种,遍历这些情况的时间复杂度是 O(N!)。
方法一:基于集合的回溯
判断一个位置所在的列和两条斜线上是否存在皇后,使用三个集合columns、diagonals1和diagonals2分别记录每一列以及两条斜线上是否存在皇后。
- 列总共有N列,每列下标从0到N-1,使用列的下标可明确表示每一列
- 从左上至右下方向斜线,位置满足:行下标与列下标之差相等
- 从左下至右上方向斜线,位置满足:行下标与列下标之和相等
每次放置皇后时,对于每个位置判断其是否在三个集合中,如果三个集合都不包含当前位置,则当前位置是可以放置皇后的位置。
1 | class Solution: |
1 | a= Solution() |
[['.Q..', '...Q', 'Q...', '..Q.'], ['..Q.', 'Q...', '...Q', '.Q..']]复杂度分析
时间复杂度:O(N!),其中 N 是皇后数量。
空间复杂度:O(N),其中 N 是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N。





