【数据结构与算法】【LeetCode】【双指针】76.最小覆盖子串

滑动窗口

题目

给你一个字符串 s 、一个字符串t 。返回 s 中涵盖t所有字符的最小子串。如果 s中不存在涵盖 t所有字符的子串，则返回空字符串 “” 。

注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"

示例2：

输入：s = "a", t = "a"
输出："a"

提示：

1 <= s.length, t.length <= 10^5
s 和 t 由英文字母组成

题解

滑动窗口思想

用l,r表示滑动窗口的左边界和右边界，通过改变l,r来扩展和收缩滑动窗口，可以想象成一个窗口在字符串上游走，当这个窗口包含的元素满足条件，即包含字符串T的所有元素，记录下这个滑动窗口的长度r-l+1，这些长度中的最小值就是要求的结果。

• 步骤一：不断增加r使滑动窗口增大，直到窗口包含了T的所有元素

• 步骤二：不断增加l使滑动窗口缩小，因为是要求最小字串，所以将不必要的元素排除在外，使长度减小，直到碰到一个必须包含的元素，这个时候不能再扔了，再扔就不满足条件了，记录此时滑动窗口的长度，并保存最小值

• 步骤三：让l再增加一个位置，这个时候滑动窗口肯定不满足条件了，那么继续从步骤一开始执行，寻找新的满足条件的滑动窗口，如此反复，直到j超出了字符串S范围。

判断窗口是否包含T中所有元素

用字典need表示当前滑动窗口中需要的各元素数量，一开始滑动窗口为空，用T中各元素初始化need，在滑动窗口扩展或者收缩时，维护该need字典

• 当窗口包含某个元素，need中该元素数量减1，表示所需元素减少1个；
• 当窗口移除某个元素，need中钙元素的数量加1

need始终记录当前滑动窗口下，还需的元素数量，在改变l,r时，需同步维护need

注意：只要某个元素包含在滑动窗口中，need中就存储这个元素的数量，如果某个元素存储的是负数表示这个元素是多余的。如need={‘A’:-2,'C':1}时，表示当前窗口中，2个A是多余的，同时还需要一个C。此目的是步骤二中排除不必要的元素，数量为负的就是不必要的元素，而数量为0表示刚刚好。

当need中所有元素的数量都小于等于0时，表示当前滑动窗口不再需要任何元素

优化

如果每次判断滑动窗口是否包含了T的所有元素，都去遍历need看是否所有元素数量都小于等于0，这个会耗费O(k)的时间复杂度，k代表字典长度，最坏情况下，k可能等于len(S)。

其实这个是可以避免的，我们可以维护一个额外的变量needCnt来记录所需元素的总数量，当我们碰到一个所需元素c，不仅need[c]的数量减少1，同时needCnt也要减少1，这样我们通过needCnt就可以知道是否满足条件，而无需遍历字典了。
前面也提到过，need记录了遍历到的所有元素，而只有need[c]>0大于0时，代表c就是所需元素

图示

以S=”DOABECODEBANC”，T=”ABC”为例

初始状态：

• 步骤一：不断增加j使滑动窗口增大，直到窗口包含了T的所有元素，need中所有元素的数量都小于等于0，同时needCnt也是0

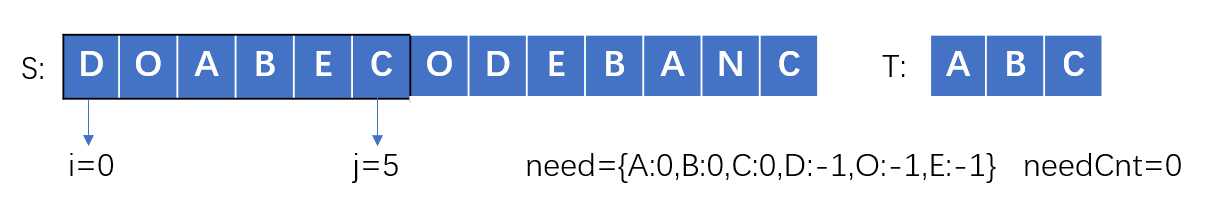
• 步骤二：不断增加i使滑动窗口缩小，直到碰到一个必须包含的元素A，此时记录长度更新结果

步骤三：让i再增加一个位置，开始寻找下一个满足条件的滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import collections
class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need=collections.defaultdict(int) # int可以用来计数，重复出现的key，对应值增加1
        for c in t:
            need[c] += 1
        needCnt= len(t)
        l=0
        res = (0,float('inf')) 
        for r,c in enumerate(s):
            if need[c]>0:
                needCnt -=1
            need[c] -=1
            
            if needCnt==0:# 步骤一：滑动窗口包含了所有T元素
                while True: # 步骤二：增加l,排除多余元素
                    c=s[l]
                    if need[c]==0:
                        break
                    need[c] +=1
                    l +=1
                if r-l<res[1]-res[0]: #记录结果
                    res=(l,r)
                need[s[l]]+=1 # 步骤三：l增加一个位置，寻找新的满足条件滑动窗口
                needCnt +=1
                l +=1
        return  '' if res[1]>len(s) else s[res[0]:res[1]+1]    #如果res始终没被更新过，代表无满足条件的结果

1
2
3
4

s = 'ADOBECODEBANC'
t = "ABC"
a= Solution()
print(a.minWindow(s,t))

BANC

复杂度

我们会用r扫描一遍S，也会用l扫描一遍S，最多扫描2次S，所以时间复杂度是O(n)，空间复杂度为O(k)，k为S和T中的字符集合。