二叉搜索查找,插入
题目
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。
示例1
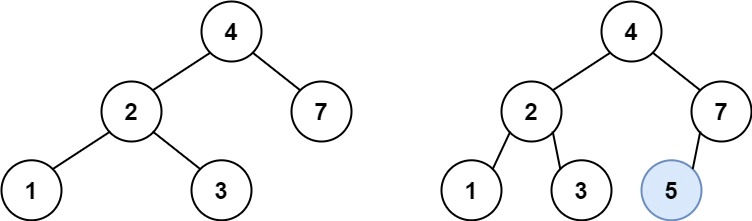
输入:root = [4,2,7,1,3], val = 5
输出:[4,2,7,1,3,5]
解释:另一个满足题目要求可以通过的树是:
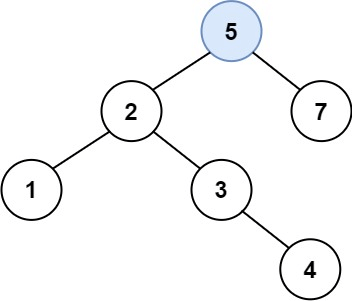
示例2
输入:root = [40,20,60,10,30,50,70], val = 25
输出:[40,20,60,10,30,50,70,null,null,25]
示例3
输入:root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出:[4,2,7,1,3,5]
题解
思路与算法
首先回顾二叉搜索树的性质:对于任意节点 root 而言,左子树(如果存在)上所有节点的值均小于root.val,右子树(如果存在)上所有节点的值均大于 root.val,且它们都是二叉搜索树。
因此,当将 val 插入到以root 为根的子树上时,根据 val 与 root.val 的大小关系,就可以确定要将val 插入到哪个子树中。
- 如果该子树不为空,则问题转化成了将 val 插入到对应子树上。
- 否则,在此处新建一个以 val 为值的节点,并链接到其父节点root 上
复杂度分析
时间复杂度:O(N),其中 N 为树中节点的数目。最坏情况下,我们需要将值插入到树的最深的叶子结点上,而叶子节点最深为 O(N)
空间复杂度:O(1)。我们只使用了常数大小的空间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
from queue import Queue
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def create_tree(list_tree):
if not list_tree:
return []
new_queue= Queue()
root = TreeNode(list_tree[0])
new_queue.put(root)
count = 1
while not new_queue.empty() and count<len(list_tree):
dequeue = new_queue.get()
if not dequeue.left and not dequeue.right:
if count<len(list_tree) and list_tree[count]:
dequeue.left=TreeNode(list_tree[count])
count= count+1
if count<len(list_tree) and list_tree[count]:
dequeue.right=TreeNode(list_tree[count])
count= count+1
if dequeue.left:
new_queue.put(dequeue.left)
if dequeue.right:
new_queue.put(dequeue.right)
return root
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
if not root:
return TreeNode(val)
pos = root
while pos:
if val < pos.val:
if not pos.left:
pos.left = TreeNode(val)
break
else:
pos = pos.left
else:
if not pos.right:
pos.right = TreeNode(val)
break
else:
pos = pos.right
return root
root = [40,20,60,10,30,50,70]
val = 25
root_tree=create_tree(root)
a=Solution()
result =a.insertIntoBST(root_tree,val)
|







