本文是对线性SVM实践性理解,利用sklearn.svm中的LinearSVC。此外参考链接给出了几个较为详细的SVM原理理解。
数据集操作
1
2
3
4
5
6
| import numpy as np
import pandas as pd
import sklearn.svm
import seaborn as sns
import scipy.io as sio
import matplotlib.pyplot as plt
|
1
2
| mat = sio.loadmat('./data/ex6data1.mat')
mat
|
{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Nov 13 14:28:43 2011',
'__version__': '1.0',
'__globals__': [],
'X': array([[1.9643 , 4.5957 ],
[2.2753 , 3.8589 ],
[2.9781 , 4.5651 ],
[2.932 , 3.5519 ],
[3.5772 , 2.856 ],
[4.015 , 3.1937 ],
[3.3814 , 3.4291 ],
[3.9113 , 4.1761 ],
[2.7822 , 4.0431 ],
[2.5518 , 4.6162 ],
[3.3698 , 3.9101 ],
[3.1048 , 3.0709 ],
[1.9182 , 4.0534 ],
[2.2638 , 4.3706 ],
[2.6555 , 3.5008 ],
[3.1855 , 4.2888 ],
[3.6579 , 3.8692 ],
[3.9113 , 3.4291 ],
[3.6002 , 3.1221 ],
[3.0357 , 3.3165 ],
[1.5841 , 3.3575 ],
[2.0103 , 3.2039 ],
[1.9527 , 2.7843 ],
[2.2753 , 2.7127 ],
[2.3099 , 2.9584 ],
[2.8283 , 2.6309 ],
[3.0473 , 2.2931 ],
[2.4827 , 2.0373 ],
[2.5057 , 2.3853 ],
[1.8721 , 2.0577 ],
[2.0103 , 2.3546 ],
[1.2269 , 2.3239 ],
[1.8951 , 2.9174 ],
[1.561 , 3.0709 ],
[1.5495 , 2.6923 ],
[1.6878 , 2.4057 ],
[1.4919 , 2.0271 ],
[0.962 , 2.682 ],
[1.1693 , 2.9276 ],
[0.8122 , 2.9992 ],
[0.9735 , 3.3881 ],
[1.25 , 3.1937 ],
[1.3191 , 3.5109 ],
[2.2292 , 2.201 ],
[2.4482 , 2.6411 ],
[2.7938 , 1.9656 ],
[2.091 , 1.6177 ],
[2.5403 , 2.8867 ],
[0.9044 , 3.0198 ],
[0.76615 , 2.5899 ],
[0.086405, 4.1045 ]]),
'y': array([[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[0],
[1]], dtype=uint8)}
1
2
3
4
5
6
| mat = sio.loadmat('./data/ex6data1.mat')
print(mat.keys())
data = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
data['y'] = mat.get('y')
data.head()
|
dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])
|
X1 |
X2 |
y |
| 0 |
1.9643 |
4.5957 |
1 |
| 1 |
2.2753 |
3.8589 |
1 |
| 2 |
2.9781 |
4.5651 |
1 |
| 3 |
2.9320 |
3.5519 |
1 |
| 4 |
3.5772 |
2.8560 |
1 |
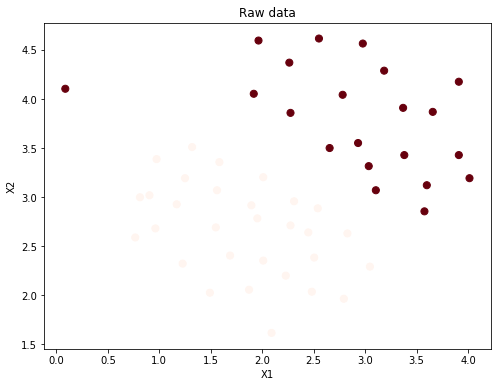
可视化data
注意左边的边界情况
1
2
3
4
5
6
| fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['y'], cmap='Reds')
ax.set_title('Raw data')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
plt.show()
|
try $C=1$
http://scikit-learn.org/stable/modules/generated/sklearn.svm.LinearSVC.html#sklearn.svm.LinearSVC
- fix(X,y): 训练模型
- predict(X): 用模型进行预测,返回预测值
- score(X,y[, sample_weight]):返回在(X, y)上预测的准确率
1
2
3
| svc1 = sklearn.svm.LinearSVC(C=1, loss='hinge')
svc1.fit(data[['X1', 'X2']], data['y'])
svc1.score(data[['X1', 'X2']], data['y'])
|
0.9803921568627451
1
2
| data['SVM1 Confidence'] = svc1.decision_function(data[['X1', 'X2']])
data.head()
|
|
X1 |
X2 |
y |
SVM1 Confidence |
| 0 |
1.9643 |
4.5957 |
1 |
0.798413 |
| 1 |
2.2753 |
3.8589 |
1 |
0.380796 |
| 2 |
2.9781 |
4.5651 |
1 |
1.372965 |
| 3 |
2.9320 |
3.5519 |
1 |
0.518512 |
| 4 |
3.5772 |
2.8560 |
1 |
0.331923 |
1
2
3
4
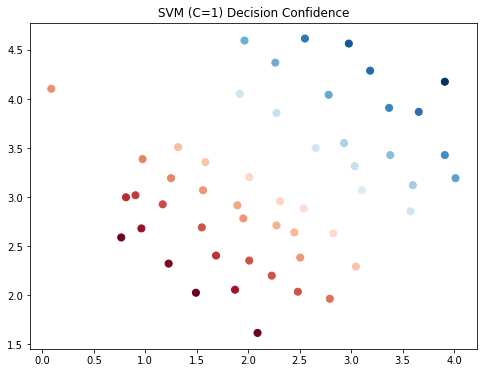
| fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM1 Confidence'], cmap='RdBu')
ax.set_title('SVM (C=1) Decision Confidence')
plt.show()
|
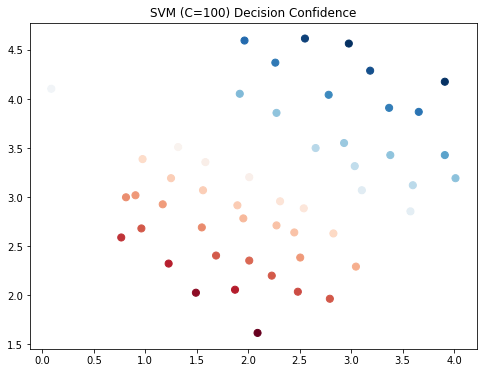
try $C=100$
对于较大的C,你会尝试过度拟合数据,所以左边的边缘情况现在被归为右边
1
2
3
| svc100 = sklearn.svm.LinearSVC(C=100, loss='hinge')
svc100.fit(data[['X1', 'X2']], data['y'])
svc100.score(data[['X1', 'X2']], data['y'])
|
0.9803921568627451
1
| data['SVM100 Confidence'] = svc100.decision_function(data[['X1', 'X2']])
|
1
2
3
4
| fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM100 Confidence'], cmap='RdBu')
ax.set_title('SVM (C=100) Decision Confidence')
plt.show()
|
|
X1 |
X2 |
y |
SVM1 Confidence |
SVM100 Confidence |
| 0 |
1.9643 |
4.5957 |
1 |
0.798413 |
3.483024 |
| 1 |
2.2753 |
3.8589 |
1 |
0.380796 |
1.652665 |
| 2 |
2.9781 |
4.5651 |
1 |
1.372965 |
4.569583 |
| 3 |
2.9320 |
3.5519 |
1 |
0.518512 |
1.502287 |
| 4 |
3.5772 |
2.8560 |
1 |
0.331923 |
0.181774 |
参考链接








