【吴恩达机器学习】练习5-方差与偏差

import numpy as np
import scipy.io as sio
import scipy.optimize as opt
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

map(lambda x, y: x + y, [1, 3, 5, 7, 9], [2, 4, 6, 8, 10])

list(map(lambda x, y: x + y, [1, 3, 5, 7, 9], [2, 4, 6, 8, 10]))

list(map(lambda x: x ** 2, [1, 2, 3, 4, 5]))

d = sio.loadmat('ex5data1.mat')
list(map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']]))

d['X'].shape

d['y']

def load_data():
    """for ex5
    d['X'] shape = (12, 1)
    pandas has trouble taking this 2d ndarray to construct a dataframe, so I ravel
    the results
    """
    d = sio.loadmat('ex5data1.mat')
    return map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']])

X, y, Xval, yval, Xtest, ytest = load_data()

df = pd.DataFrame({'water_level':X, 'flow':y})#字典构造 ：数据帧(DataFrame)是二维数据结构，即数据以行和列的表格方式排列
df

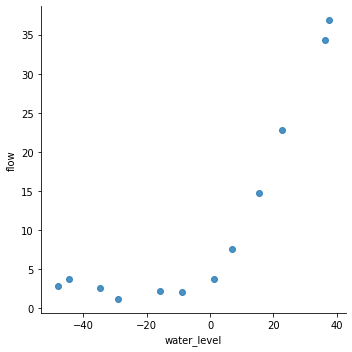
sns.lmplot('water_level', 'flow', data=df, fit_reg=False, size=5)
plt.show()

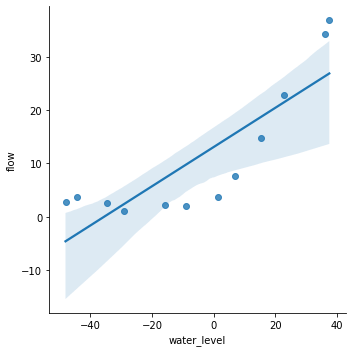
sns.lmplot('water_level', 'flow', data=df, fit_reg=True, size=5)
plt.show()

X, Xval, Xtest = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]

X

def cost(theta, X, y):
    """
    X: R(m*n), m records, n features
    y: R(m)
    theta : R(n), linear regression parameters
    """
    m = X.shape[0]

    inner = X @ theta - y  # R(m*1)

    # 1*m @ m*1 = 1*1 in matrix multiplication
    # but you know numpy didn't do transpose in 1d array, so here is just a
    # vector inner product to itselves
    square_sum = inner.T @ inner
    cost = square_sum / (2 * m)

    return cost

def cost(theta, X, y):
    m = X.shape[0]
    
    inner = X@ theta - y
    
    square_sum = inner.T@ inner
    cost = square_sum / (2*m)
    return cost

theta = np.ones(X.shape[1])

cost(theta, X, y)

a = np.array([[1,3],[2,4]])
b = np.array([[2,1],[3,3]])
a @ b

def gradient(theta, X, y):
    m = X.shape[0]

    inner = X.T @ (X @ theta - y)  # (m,n).T @ (m, 1) -> (n, 1)

    return inner / m

gradient(theta, X, y)

# L2-norm
def regularized_gradient(theta, X, y, l=1):
    m = X.shape[0]

    regularized_term = theta.copy()  # same shape as theta 产生与theta相同的shape
    regularized_term[0] = 0  # don't regularize intercept theta 截距不正则化

    regularized_term = (l / m) * regularized_term

    return gradient(theta, X, y) + regularized_term

regularized_gradient(theta, X, y)

def linear_regression_np(X, y, l=1):
    """linear regression
    args:
        X: feature matrix, (m, n+1) # with incercept x0=1
        y: target vector, (m, )
        l: lambda constant for regularization

    return: trained parameters
    """
    # init theta
    theta = np.ones(X.shape[1])

    # train it
    res = opt.minimize(fun=regularized_cost,
                       x0=theta,
                       args=(X, y, l),
                       method='TNC',
                       jac=regularized_gradient,
                       options={'disp': True})
    return res

def regularized_cost(theta, X, y, l=1):
    m = X.shape[0]

    regularized_term = (l / (2 * m)) * np.power(theta[1:], 2).sum()

    return cost(theta, X, y) + regularized_term

theta = np.ones(X.shape[0])

final_theta = linear_regression_np(X, y, l=0).get('x')

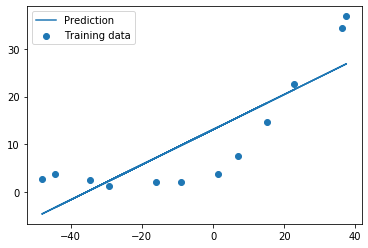
b = final_theta[0] # intercept
m = final_theta[1] # slope

plt.scatter(X[:,1], y, label="Training data")
plt.plot(X[:, 1], X[:, 1]*m + b, label="Prediction")
plt.legend(loc=2)
plt.show()

training_cost, cv_cost = [], []

m = X.shape[0]
for i in range(1, m+1):
#     print('i={}'.format(i))
    res = linear_regression_np(X[:i, :], y[:i], l=0)
    
    tc = regularized_cost(res.x, X[:i, :], y[:i], l=0)
    cv = regularized_cost(res.x, Xval, yval, l=0)
#     print('tc={}, cv={}'.format(tc, cv))
    
    training_cost.append(tc)
    cv_cost.append(cv)

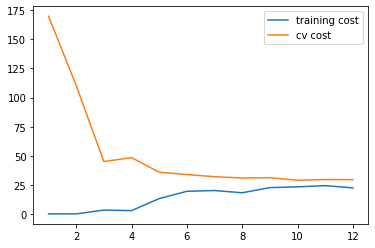
plt.plot(np.arange(1, m+1), training_cost, label='training cost')
plt.plot(np.arange(1, m+1), cv_cost, label='cv cost')
plt.legend(loc=1)
plt.show()

def prepare_poly_data(*args, power):
    """
    args: keep feeding in X, Xval, or Xtest
        will return in the same order
    """
    def prepare(x):
        # expand feature
        df = poly_features(x, power=power)

        # normalization
        ndarr = normalize_feature(df).as_matrix()

        # add intercept term
        return np.insert(ndarr, 0, np.ones(ndarr.shape[0]), axis=1)

    return [prepare(x) for x in args]

def poly_features(x, power, as_ndarray=False):
    data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)}
    df = pd.DataFrame(data)

    return df.as_matrix() if as_ndarray else df

X, y, Xval, yval, Xtest, ytest = load_data()

data = {'f{}'.format(i): np.power(X, i) for i in range(1, 3 + 1)}
df = pd.DataFrame(data)
df

# 调用准备多项式中回归数据中的normalize_feature()函数 标准化
normalize_feature(df).as_matrix()

poly_features(X, power=3)

def normalize_feature(df):
    """Applies function along input axis(default 0) of DataFrame."""
    return df.apply(lambda column: (column - column.mean()) / column.std())# mean平均值，std标准差

X_poly, Xval_poly, Xtest_poly= prepare_poly_data(X, Xval, Xtest, power=8)
X_poly[:3, :]

def plot_learning_curve(X, y, Xval, yval, l=0):
    training_cost, cv_cost = [], []
    m = X.shape[0]

    for i in range(1, m + 1):
        # regularization applies here for fitting parameters
        res = linear_regression_np(X[:i, :], y[:i], l=l)

        # remember, when you compute the cost here, you are computing
        # non-regularized cost. Regularization is used to fit parameters only
        tc = cost(res.x, X[:i, :], y[:i])
        cv = cost(res.x, Xval, yval)

        training_cost.append(tc)
        cv_cost.append(cv)

    plt.plot(np.arange(1, m + 1), training_cost, label='training cost')
    plt.plot(np.arange(1, m + 1), cv_cost, label='cv cost')
    plt.legend(loc=1)

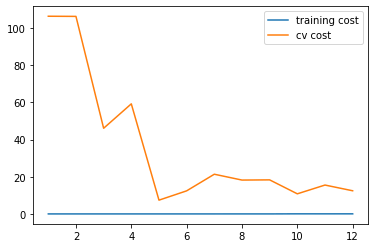
plot_learning_curve(X_poly, y, Xval_poly, yval, l=0)
plt.show()

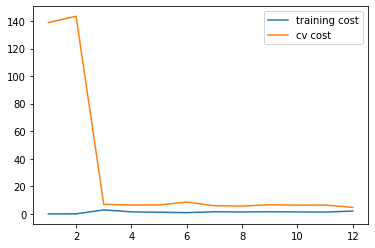
plot_learning_curve(X_poly, y, Xval_poly, yval, l=1)
plt.show()

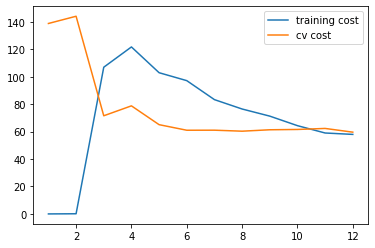
plot_learning_curve(X_poly, y, Xval_poly, yval, l=100)
plt.show()

l_candidate = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost, cv_cost = [], []

for l in l_candidate:
    res = linear_regression_np(X_poly, y, l)
    
    tc = cost(res.x, X_poly, y)
    cv = cost(res.x, Xval_poly, yval)
    
    training_cost.append(tc)
    cv_cost.append(cv)

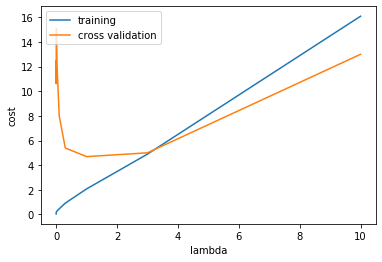
plt.plot(l_candidate, training_cost, label='training')
plt.plot(l_candidate, cv_cost, label='cross validation')
plt.legend(loc=2)

plt.xlabel('lambda')

plt.ylabel('cost')
plt.show()

# best cv I got from all those candidates
l_candidate[np.argmin(cv_cost)]

# use test data to compute the cost
for l in l_candidate:
    theta = linear_regression_np(X_poly, y, l).x
    print('test cost(l={}) = {}'.format(l, cost(theta, Xtest_poly, ytest)))